- 給忙碌青少年講人工智能:會思考的機器和AI時代
- (英)《新科學家》雜志編著
- 3179字
- 2025-06-05 14:23:56
阿蘭·圖靈與計算機信息處理技術(shù)的出現(xiàn)
阿蘭·圖靈的思想塑造了我們的世界。他為現(xiàn)代計算機和信息計算革新奠定了基礎(chǔ),并對人工智能、大腦乃至發(fā)育生物學做出了頗有遠見的預測。“二戰(zhàn)”期間,他還為盟軍工作,完成了至關(guān)重要的密碼破譯。
為了理解圖靈的成就對于今天的重要性,我們首先要介紹他如何著手解決那個時代最大的數(shù)學難題之一,以及在該過程中如何為所有計算機的基礎(chǔ)完成了定義。而人工智能正是隨著計算機信息處理技術(shù)的出現(xiàn),發(fā)展而來。
首臺計算機問世
“二戰(zhàn)”之前,“計算機”(computer)一詞是指手動或在機械式算數(shù)機的輔助下進行計算的某個人,通常是女性。這些人類計算機是工業(yè)革命的重要組成部分,她們經(jīng)常要進行重復乏味的計算,比如編寫對數(shù)表所需的那類計算。
但在1936年,年僅24歲的圖靈為一種新型計算機的誕生奠定了基礎(chǔ)(時至今日,我們依然承認這一點),他在信息技術(shù)革新中發(fā)揮了開創(chuàng)性作用。不過,圖靈并未著手發(fā)明、設(shè)計現(xiàn)代計算機模型。最初,他只是希望解決數(shù)學邏輯中的某個難題。20世紀30年代中期,他攻克了令人望而生畏的“判定問題”,該難題由數(shù)學家大衛(wèi)·希爾伯特(David Hilbert)于1928年提出。
當時,數(shù)學家們正在完善明確具體的基礎(chǔ)數(shù)學,希爾伯特想要知道,是否所有的數(shù)學命題都是“可判定的”,如2+2=4。換言之,是否存在一個循序漸進的判定法,可以確定任何給定的數(shù)學命題是真是假?這是數(shù)學家研究的基本問題。雖然斷言像2+2=4這樣的命題為真很容易,但復雜的邏輯命題判定起來其實相當棘手。以波恩哈德·黎曼于1859年提出黎曼猜想為例,他對質(zhì)數(shù)在自然數(shù)中的分布做出了具體預測,數(shù)學家們懷疑其為真,但至今依然無法確定。
如果能夠找到希爾伯特構(gòu)想的循序漸進判定法,那將意味著,人們最終可以設(shè)計發(fā)明某種機器,為數(shù)學家們想要測試的任何邏輯命題提供確切的答案。所有懸而未決的數(shù)學難題都能得以解決。希爾伯特尋找的其實是一種編程語言,然而在20世紀30年代,計算機和計算機語言都不存在,所以當時沒人意識到它的局限性。如今,我們將他的循序漸進的判定法稱為“算法”。圖靈必須定義“計算”這個概念本身,以攻克“判定問題”。
1936年,圖靈發(fā)表了一篇論文。為希爾伯特的問題給出了明確答案:沒有程序可以判定任何給定數(shù)學命題的真假。此外,很多尚未解決的重要數(shù)學問題都是“不可判定的”。這對人類數(shù)學家來說是個好消息,他們由此判定,自己永遠不會被機器取代。但憑借他的論文,圖靈的成就不僅僅是解決了希爾伯特的問題,為了證明自己的結(jié)論,圖靈在論文里提出了現(xiàn)代計算機的理論基礎(chǔ)。
在測試希爾伯特的想法正確與否之前,圖靈需要定義何謂循序漸進判定法,以及構(gòu)想出一種執(zhí)行該方法的設(shè)備。他雖不需制造這樣的機器,但確實有必要假想并陳述其工作原理。
首先,他構(gòu)想了一臺能夠從紙帶上讀取符號的機器(見圖1.1)。你可以將紙帶送入,機器會檢查符號,然后依據(jù)一套內(nèi)部規(guī)則來繼續(xù)工作。例如,它可以將寫在紙帶上的兩個數(shù)字相加,然后在紙帶后邊打印出結(jié)果。后來人們將其稱為圖靈機。然而,由于每臺圖靈機都有預先設(shè)定的內(nèi)部規(guī)則(實質(zhì)上是一段固定程序),所以它不能用于測試希爾伯特的問題。
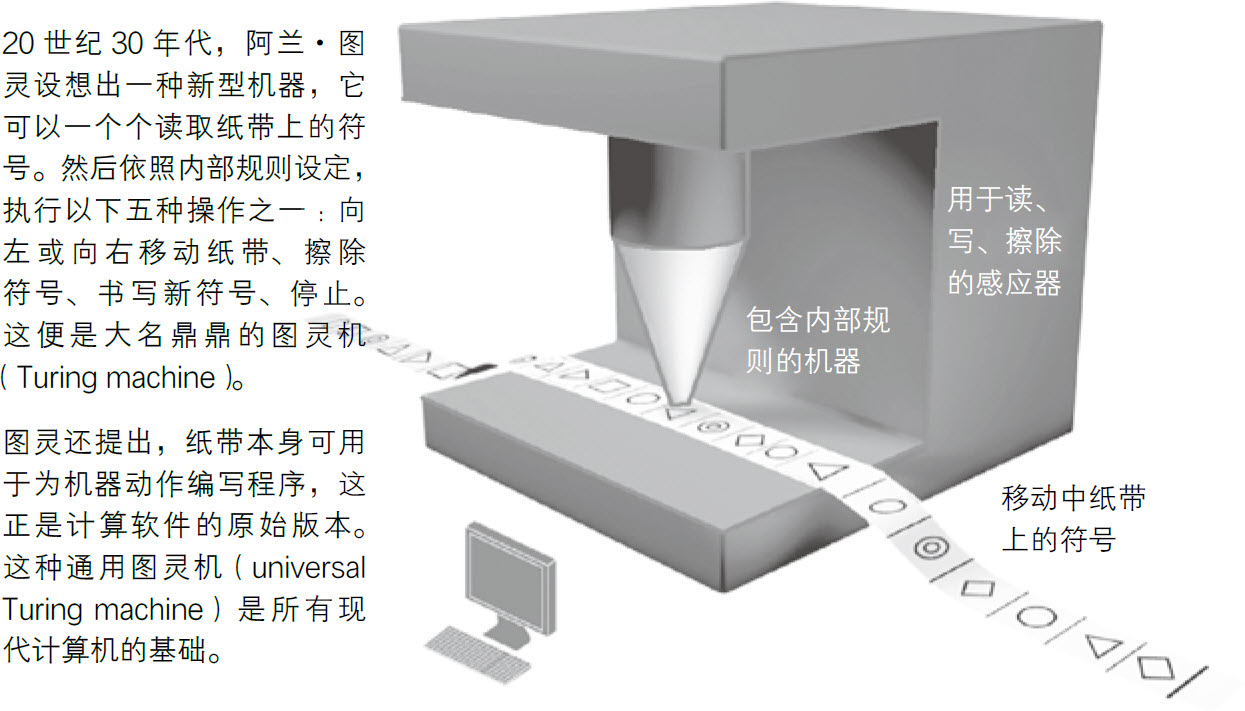
圖1.1 圖靈從未真正用他的理論制造出一臺計算機器,但其理論仍然是如今所有標準計算機的基石
圖靈意識到,有可能制造出一種這樣的機器,機器最初可從紙帶上讀取一段程序,并用該程序定義其內(nèi)部規(guī)則。借由這種做法,它就具備編程功能,可以與任何含有固定內(nèi)部規(guī)則的單獨圖靈機執(zhí)行相同的動作。我們將這種靈活的設(shè)備稱為通用圖靈機,它其實就是計算機。
這是如何實現(xiàn)的?寫在紙帶上的程序可以看作軟件。圖靈的通用機器本質(zhì)上就是加載紙帶上的軟件,正如我們現(xiàn)今從硬盤上調(diào)用程序:你的計算機既可以是文字處理器,也可以是音樂播放器。
計算的局限性
一旦圖靈擁有了這臺理論計算機,他就能根據(jù)計算機能做什么,不能做什么,來回答什么是“可計算的”。
為了證明希爾伯特提出的方法不存在,圖靈只需找到一條計算機無法完成計算的邏輯命題。為此他提出了一個具體問題:如果任由程序運行,計算機是否能完成計算,或永遠運行下去?換言之,計算機能否判定“程序完成時停止運行”這一命題是真是假?他證明出,答案是“不能”。因此,希爾伯特的“判定問題”得以解決。圖靈結(jié)論最終證明,計算機無法完成所有事情。
在圖靈努力解決“判定問題”的同時,美國數(shù)學家阿隆索·丘奇(Alonzo Church)則采用純數(shù)學方法嘗試解決該問題。二人幾乎同時發(fā)表了論文。圖靈的文章定義了“可計算性”這一概念,而丘奇給出了“有效可計算性”的定義。兩者異曲同工。這個結(jié)果,即丘奇-圖靈的論點,是我們認識到計算機具有局限性的基礎(chǔ),并在深奧的數(shù)學邏輯問題與你的臺式或筆記本電腦之間建立了直接關(guān)聯(lián)。
即使計算機越來越先進,但它們依然處在丘奇和圖靈提出的局限性下。相比20世紀40年代的龐然大物,盡管現(xiàn)代計算機具有令人驚嘆的強大能力,但它們依然只能執(zhí)行在通用圖靈機上就能完成的任務(wù)。
人工大腦
圖靈對人類大腦也很好奇。他相信可以在計算機上模擬嬰兒的大腦。1948年,他撰寫了一份報告來闡釋自己的理論,并對當下用于模擬神經(jīng)元的人工神經(jīng)網(wǎng)絡(luò)給出了早期描述。
他的論文很有先見之明,但直到1968年才得以發(fā)表(那時他已去世14年之久),部分原因是,他在英國國家物理實驗室的導師查爾斯·高爾頓·達爾文(Charles Galton Darwin)將其稱為“小學生作文”。該論文描述了一種大腦模型,其基于“神經(jīng)元”這一加工單元。神經(jīng)元可接受兩個輸入,且只有一個輸出。它們以隨機方式連接在一起,形成龐大的互聯(lián)單元網(wǎng)絡(luò)。在互聯(lián)載體(相當于大腦突觸)上傳遞的信號由“1”或“0”組成。現(xiàn)今人們稱之為“布爾神經(jīng)網(wǎng)絡(luò)”,不過圖靈當年把它叫作“無組織A型機器”。
由于A型機器本身無法學習,所以圖靈將其作為可受教的B型機器的基礎(chǔ)。B型機器神經(jīng)元之間的互聯(lián)通路配有開關(guān),這些開關(guān)可接受“教育”,除此之外,它與A型機器完全相同。這種教育體現(xiàn)為命令開關(guān)打開(允許信號經(jīng)突觸傳遞)或關(guān)閉(阻斷信號)。圖靈的理論指出,這樣的教育能夠用于調(diào)校神經(jīng)元網(wǎng)絡(luò)。
圖靈去世后,人們開始重新審視他的理論,而事實證明,他的簡單的基于二進制的神經(jīng)網(wǎng)絡(luò)是具備學習能力的。例如,它們能學會識別像“O”和“X”這樣的簡單形狀圖案。后來,獨立而復雜的神經(jīng)網(wǎng)絡(luò)成為人工智能的研究焦點,從自動駕駛汽車到面部識別系統(tǒng),一切成功案例的背后,都有它的存在。不過,它現(xiàn)在更廣為人知的名字是“符號推理”技術(shù)。
圖靈:戛然而止的生命
毋庸置疑,阿蘭·圖靈是20世紀最偉大的智者之一。《自然》期刊稱贊他是“有史以來頂尖的科學家之一”。大眾對這個評價也心悅誠服。
從本質(zhì)上來講,是圖靈創(chuàng)立了計算機科學。而他還憑借辛勤的工作和一系列洞見,幫助盟軍贏得了“二戰(zhàn)”。此外,他還提出了關(guān)于智能的本質(zhì)及其與大腦結(jié)構(gòu)相關(guān)聯(lián)的基本問題。在生命的最后階段,他從事生物學方面的一些工作同樣值得關(guān)注。他研究出了“形態(tài)建成”的數(shù)學理論(比如現(xiàn)實中豹子是如何長出斑點的),這為生物學中的某個領(lǐng)域奠定了基礎(chǔ)。而直到現(xiàn)在,該領(lǐng)域才得到充分的重視。但在1954年,在被判有“嚴重猥褻罪”后,圖靈結(jié)束了自己的生命,他那涉及面廣泛、新穎而深刻的思想就此隕落。圖靈在生活中確實是一名同性戀者,而這在當時的英國是非法的。
圖靈去世的時候,計算機尚處于嬰兒期,體態(tài)龐大而笨重。弗朗西斯·克里克(Francis Crick)和詹姆斯·沃森(James Watson)則剛剛揭開了DNA(脫氧核糖核酸)結(jié)構(gòu)之謎,而人工智能甚至還沒有名字。20世紀70年代之前,圖靈一直默默無聞,關(guān)于他的記載相對稀少,一部分是因為他的同性戀和自殺行為,另一部分在于他的論文涉及深奧的數(shù)學,以及他在布萊切利公園(1)工作時的保密性。
1967年,同性戀在英國合法化后,布萊切利公園的秘密繼而浮出水面,圖靈留下的知識遺產(chǎn)開始得到認可。如今再回顧他41年的生命及其對世界持續(xù)的影響,我們也只能猜測,如果他經(jīng)歷足夠漫長且豐富多彩的生活,他那獨特的思想不知能達到何等高度。