1.2.1　數制與轉換

1.數制

數制是數的表示及計算的方法。數值數據是有大小的，人們習慣采用的是十進制。但在計算機內，各種信息都是以二進制代碼形式表示的，這是因為采用二進制表示信息物理器件容易實現，并且二進制數據運算簡單，可靠性高、能用性強。在設計研究計算機時常采用八進制、十六進制。

（1）十進制計數制

基數：10。

數碼：0、1、2、3、4、5、6、7、8、9。

位權：以10為底的冪。

進位規則：逢十進一。

十進制是人們最習慣使用的一種進位計數制。

（2）二進制計數制

基數：2。

數碼：0、1。

位權：以2為底的冪。

進位規則：逢二進一。

二進制是計算機中最常用數制。

（3）八進制計數制

基數：8。

數碼：0、1、2、3、4、5、6、7。

位權：以8為底的冪。

進位規則：逢八進一。

（4）十六進制計數制

基數：16

數碼：0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。

位權：以16為底的冪。

進位規則：逢十六進一。

在計算機中，通常用數字后面跟一個英文字母表示該數進位計數制。十進制數一般用D（Decimal）或d、二進制用B（Binary）或b、八進制用O（Octal）或o、十六進制數用H（Hexadecimal）或h。

2.轉換

人們習慣采用十進制數，計算機采用的是二進制數，書寫時又多采用八進制數或十六進制數，因此，必然產生各種進位計數制之間的相互轉換問題。

（1）任意進制數（用R表示）轉換為十進制數

位權相加法：把R進制數每位上的權數與該位上的數碼相乘，然后求和即得要轉換的十進制數。即：

【例1.2.1-1】將二進制數10111轉換成十進制數。

（10111）2=1×24+0×23+1×22+1×21+1×20=16+0+4+2+1=（23）10

【例1.2.1-2】將八進制數127轉換成十進制數。

（127）8=1×82+2×81+7×80=64+16+7=（87）10

【例1.2.1-3】將十六進制數15B轉換成十進數。

（15B）16=1×162+5×161+11×160=256+80+11=（347）10

（2）十進制數轉換為R進制數

轉換方法：將十進制轉換成R進制時，需對整數部分和小數部分進行分別處理。

①整數部分連續除以R，其余數的序列就是對應的進位計數制的整數部分。

②小數部分連續乘以R，取其整數構成的序列就是對應的進位計數的小數部分。

【例1.2.1-4】將十進制數44.125轉換成二進制數。

轉換結果：（44.125）10=（101100.001）2

【例1.2.1-5】將十進制數44.125轉換成八進制數。

轉換結果：（44.125）10=（54.1）8

【例1.2.1-6】將十進制數44.125轉換成十六進制數。

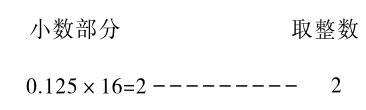
轉換結果：（44.125）10=（2C.2）16

（3）二進制與八進制、十六進制數之間的轉換

大家知道，23=8、24=16，也就是說，1個八進制位等于3個二進制位，1個十六進制位等于4個二進制位。因此，很容易實現二進制與八進制、十六進制之間的轉換。

①二進制轉換成八進制或十六進制。

轉換方法：從小數點開始，向左或向右每3位或4位二進制數分成一組（不足位數，整數部分高位補0，小數部分低位補0），然后按對應位置寫出每組二進制數等值的八進制數或十六進制數。

【例1.2.1-7】將二進制數10011010110轉換成八進制數。

轉換結果：（10011010110）2=（2326）8

【例1.2.1-8】將二進制數1001.1010110轉換成十六進制數。

轉換結果：（1001.1010110）2=（9.AC）16

②八進制或十六進轉換成制二進制。

轉換方法：將每位八進制或十六進制數用3位或4位二進制數代替即可，小數點不動。

【例1.2.1-9】將八進制數7153轉換成二進制數。

轉換結果：（7153）8=（111001101011）16

【例1.2.1-10】將十六進制數9A28轉換成二進制數。

轉換結果：（9A28）16=（1001101000101000）2

（4）八進制與十六進制數之間的轉換

八進制與十六進制數之間不能直接轉換，它們之間可通過二進制間接來實現轉換。

【例1.2.1-11】將八進制數476轉換成十六進制數。

（476）8=（100111110）2=（13E）16

【例1.2.1-12】將十六進制數3C45轉換成八進制數。

（3C45）16=（0011110001000101）2=（36105）8

各種進制數對照表如表1.2.1所示。